[C] 이진 탐색 트리(Binary Search Tree, BST) 개념 및 구현

[ 크래프톤정글/C 언어 ]

2022년 11월 28일 21시 38분 06초에 업로드 된 글입니다.

작성자: nickhealthy

이진 탐색 트리(Binary Search Tree, BST)

원소를 특정한 조건에 따라 정렬해 놓은 이진트리를 말한다. 이진 탐색 트리는 탐색을 위해 정렬을 해놓은 트리이다.

이진 탐색 트리는 검색 수행 연산은 O(logN) 이다.

이진 탐색 트리의 속성

모든 원소는 유일한 키 값을 갖는다.
- 즉, 중복된 내용을 가지는 항목은 없다.
왼쪽 서브트리의 모든 원소들은 루트의 키보다 작은 값을 갖는다.
오른쪽 서브트리의 모든 원소들은 루트의 키보다 큰 값을 갖는다.
왼쪽 서브트리와 오른쪽 서브트리도 이진탐색트리이다.
- 즉, 일반 트리나 이진트리하고 똑같이 이진탐색트리도 재귀적인 정의를 한다.(서브트리에서 볼 때나 루트노드에서 볼 때나 위의 조건은 모두 성립되므로)
- 트리 안에서 어떤 노드를 루트로 잡던지 위 조건은 항상 true가 된다.

또한 이진 탐색트리는 '중위순회'로 트리를 순회하게 될 때, 값이 오름차순으로 정렬되는 것을 볼 수 있다.

중위순회는 왼쪽 - 루트 - 오른쪽 순으로 순회를 하게 되는데 마찬가지로 이진 탐색 트리는 왼쪽 - 루트 - 오른쪽으로 값이 정렬되어 있기 때문에 오름차순으로 정렬되게 된다.

초기 구현 코드

#include <stdio.h>
#include <stdlib.h> // malloc를 사용하기 위해 헤더 추가

typedef char data;
// 자기참조구조체 - 데이터 부와 링크부 2개가(left, right) 들어가게 된다.
typedef struct _NODE
{
    char key;
    struct _NODE *left, *right;
} NODE;

int main(void)
{

    return 0;
}

Operator

이진 탐색 트리에서 가장 대표적인 연산들은 다음과 같다.

삽입: 이진 탐색 트리에 노드를 삽입한다. 삽입된 이후에도 이진 탐색 트리의 속성을 유지해야 한다.
삭제: 이진 탐색 트리에 노드를 삭제한다. 삭제된 이후에도 이진 탐색 트리의 속성을 유지해야 한다.
탐색: 이진 탐색 트리에서 특정 노드를 탐색한다. 탐색이 되면 해당 노드를 반환하고, NULL이 될 때까지 노드를 못찾을 시 해당 노드는 존재하지 않으므로 NULL를 return 한다.

탐색 구현

이진 탐색 트리에서 가장 근본이 되는 연산은 탐색이기 때문에 탐색 먼저 구현!

탐색에서는 3가지 케이스가 존재하게 된다.

현재 노드와(여기서는 root 매개변수로 받아 p로 처리함) 찾을 값(x)와 값이 같다면 값을 찾은 것이므로 그대로 return
현재 노드보다 찾을 값이 크다면 현재 노드를 오른쪽으로 이동(오른쪽으로 이동할수록 값이 커지기 때문에)
현재 노드보다 찾을 값이 작다면 현재 노드를 왼쪽으로 이동(왼쪽으로 이동할수록 값이 작아지기 때문에)

탐색 구현 코드

searchBST(NODE *root, char x)
{
    NODE *p = root;
    while (p != NULL)
    {
        if (p->key == x)
        {
            return p;
        }
        else if (p->key < x)
        {
            p = p->right;
        }
        else
        {
            p = p->left;
        }
    }
    return NULL;
}

삽입 구현

삽입도 탐색 구현에서 조금만 더 추가하면 삽입 연산으로 바로 구현할 수 있다.

우선 이진 탐색 트리에서는 '트리의 각 원소는 유일해야 한다'라는 속성이 있었는데, 먼저 우리가 삽입할 노드의 값이 트리에 있는지 확인을 먼저 진행해야한다. 만약 탐색을 진행하다가 원소를 찾았다면, 트리는 현재 노드의 값을 가지고 있는 것이므로 바로 해당 노드를 반환해주면 되고, 만약 원소를 찾지 못하였을 때는 해당 노드가 트리 내부에 존재하지 않은 것이므로 비로소 삽입을 진행할 수 있게 된다.

그리고 이제 삽입 구현은 탐색 구현에서 조금만 더 추가하면 된다고 했는데 결론부터 말하자면 현재 노드의 바로 이전 노드를 저장하는 parent 포인터를 갖도록 만들면 된다. 위에서 탐색에 실패하였을 때 우리는 원소를 삽입할 수 있었는데 탐색에 실패했다는 말은 똑같은 말로 현재 노드 p가 NULL의 값을 만나면 되는 것이다. 하지만 탐색 구현부에서는 원소를 찾지 못했을 때 바로 NULL를 반환하게되므로 우리가 값을 이용할 수 없지만, 삽입 구현부에서는 parent라는 포인터 변수를 할당해 현재 노드 p가 NULL를 만나는 시점에서 parent의 바로 뒤(왼쪽 혹은 오른쪽)에 삽입하면 되는 것이다.

위의 말을 간단하게 말하면 '현재 노드 p가 한 발짝 움직일 때마다 움직이기 전의 p값을 parent에 저장하면서 움직이면 된다'

조금 더 상세한 내용은 아래 주석을 참고하면 도움이 될 것 같다.

삽입 구현 코드

// 매개변수 : NODE의 포인터, 삽입할 노드의 key
NODE* insertBST(NODE* root, char x)
{
    NODE* p = root;
    // root가 NULL 일수도 있으므로 parent를 바로 root의 값을 참조하는 것이 아닌, NULL 값으로 초기화를 진행한다.
    NODE* parent = NULL;
    while (p != NULL) {
        parent = p; // p의 발자취를 따라가면서 parent에 p의 이전 값을 담음
        if (p->key == x)
            return p;
        else if (p->key < x)
            p = p->right;
        else
            p = p->left;
    }

    // 탐색에 실패하였을 때, 비로소 삽입할 수 있는 시점
    // 새 노드 할당
    NODE* newNODE = (NODE*)malloc(sizeof(NODE));
    newNODE->key = x;                      // 삽입할 key값
    newNODE->left = newNODE->right = NULL; // 단말 노드가 될 것이기 때문에 left, right NULL 값을 넣는다.

    // parent의 자식으로 새 노드 붙이기
    /*
    root가 NULL 일수도 있으므로 parent가 NULL이 아닐경우에만 삽입 과정을 수행한다.
    root가 NULL 이라면 위의 while문을 한번도 돌지 않을 것이고(같은 말로 탐색을 한번도 수행을 하지 않을 것이고),
    탐색을 한번도 수행하지 않았다면 parent의 값도 NULL로 되어있음
    */

    if (parent != NULL) {
        // 왼쪽, 오른쪽 삽입 위치 구분
        if (parent->key < newNODE->key)
            parent->right = newNODE;
        else
            parent->left = newNODE;
    }
    return newNODE;
}

삭제 구현

이진탐색트리에서의 노드 삽입, 삭제는 삽입이나 삭제한 이후에도 이진탐색트리의 모양을 유지해야 되기 때문에 어려운 것인데 그런면에서 삽입보다는 삭제가 조금 더 까다롭다. 왜냐하면 삽입은 단말 노드로만 붙이기 때문에 이진탐색트리의 모양이 유지되도록 붙이기만 하면 됐었는데, 노드 삭제라는 것은 중간에 있는 노드가 빠질 수도 있기 때문에 조금 더 복잡해지게 된다.

다음은 노드 삭제의 3가지 CASE이다.

차수가 0인 노드를 삭제하는 CASE
차수가 1인 노드를 삭제하는 CASE
차수가 2인 노드를 삭제하는 CASE

💡

차수란?

차수는 현 노드에서 자식의 수를 의미한다.

이진 탐색 트리에서는 자식이 최대 2개이다.

차수가 0인 삭제 구현 코드

차수가 0인 경우를 찾는 것은 어떻게 하면 될까? 간단하게 노드 당 left, right의 링크부 2개를 가지게 된다. 기본적으로 차수가 0이라는 것은 단말 노드가 되는 것이기 때문에 left, right의 값이 모두 NULL로 삽입 함수에서 초기화되므로 차수가 0인 노드는 현재 노드(p) 의 left, right 값이 모두 NULL 값을 가지고 있는지를 가지고 판별하면 된다.

또한 차수가 0인 노드를 삭제하는 경우 2가지의 대분류로 나뉘게 된다.

root를 삭제하는 경우
- root를 삭제하는 경우에는 parent의 값이 NULL로 유지될 것이고, root의 값을 NULL로 초기화 시켜준다.
  - parent의 값이 NULL인 이유는 while 문을 안돌기 때문인데, 왜 한번도 돌지 않을까? 현재 노드(p)는 주소값을 가지고 있을 것이기 때문에 NULL이 아닌 조건은 참이지만, root 노드 하나만 트리에 남겨져 있고 우리가 찾는 값이 일치한다면 즉, while 문의 'p->key != x' 이 부분이 거짓으로 판별나면서 while 문을 돌지 않게되고 parent는 처음 초기화해준 NULL 값을 유지하게 될 것이다.
root가 아닌 차수가 0인 노드를 삭제하는 경우
- root가 아닌 차수가 0인 노드를 삭제하는 경우에는 삭제될 대상 parent의 left, right 중에서 삭제될 노드의 주소값을 담고 있을 것이다. 따라서 parent->left == p or parent->right ==p 로 판별하게 된다.

// 매개변수 : NODE의 포인터, 삽입할 노드의 key
NODE *deleteBST(NODE *root, char x)
{
    NODE *p = root;
    // root가 NULL 일수도 있으므로 parent를 바로 root의 값을 참조하는 것이 아닌, NULL 값으로 초기화를 진행한다.
    NODE *parent = NULL;
    while ((p != NULL) && (p->key != x)) // 찾는 노드가 없다는 걸 확인한 것도 아니고, 키를 찾은 것도 아닌 동안은 계속 반복
    {
        parent = p; // p의 발자취를 따라가면서 parent에 p의 이전 값을 담음
        if (p->key < x)
        {
            p = p->right;
        }
        else
        {
            p = p->left;
        }
    }
    // 찾는 노드가 없을 땐
    // 노드 찾는데 실패했기 때문에 받은 그대로를 반환해준다.
    if (p == NULL)
    {
        printf("찾는 노드가 없습니다.\n");
        return root;
    }

    // 차수가 0인 경우(2가지 대분류 필요)
    // 1. root 를 삭제하는 경우
    // 2. root 가 아닌 노드를 삭제하는 경우
    if (p->left == NULL && p->right == NULL)
    {
    	// 현재 노드가 root 인 경우
        // 91번째 라인 'p->key != x' 의 찾는 값이 일치하여서 while문을 돌지 않게된다면, parent의 값은 NULL로 유지하게 된다.
        // 즉, 간단하게 말하면 root노드의 차수가 0이라면 parent의 값은 NULL임
        if (parent == NULL)
        {
            root = NULL;
        }
        // 루트가 아닌데 차수가 0인 경우
        // 그 이외의 경우에는 즉, 루트가 아닌 노드가 삭제될 경우에는 parent의 포인터를 고쳐주어야 한다.
        // parent가 삭제될 노드의 left 또는 right로 현재 노드(p)를 가리키고 있다.
        else
        {
            if (parent->left == p)
            {
                parent->left = NULL;
            }
            else
            {
                parent->right = NULL;
            }
        }

        free(p);	// 차수가 0, 1, 2 어떤 경우이든 간에 노드를 삭제하니까 해당 노드를 삭제한다.
    }
}

차수가 1인 삭제 구현 코드

결론부터 말하자면 삭제할 노드를 삭제하고, 삭제한 노드의 parent에 서브트리를 붙이면 된다. 그러면 서브트리는 한 레벨 위로 올라오게 된다.

아래의 이미지를 먼저 보자. 우선 차수가 1인 노드이자 삭제할 노드는 '12' 이다.

차수가 1인 노드를 삭제하는 방법은 왼쪽 또는 오른쪽 자식 노드를 가졌을텐데(여기서는 '15'인 오른쪽 자식을 가졌다), 그 자식을 바로 12의 parent인 '10' 노드한테 연결해주면 된다. 그러면 '15, 14, 20' 으로 이루어진 서브트리 전체가 한 레벨 위로 올라오면서 삭제된 노드를 빼고 직접 parent에 붙게되면서 이진 탐색 트리의 속성을 모두 갖추게 된다.

차수가 1인 즉, 특정 노드가 삭제되고 그 노드의 부모가 (기존에는 삭제된 노드의 - 그림에서는 '15'를 뜻한다.)유일한 자식을 직접 가리킬 수 있도록 해야하므로 child의 값을 저장해주어야 한다.

또한 차수가 1인 경우를 삭제해도 root 노드를 삭제하는 경우, root 노드가 아닌 노드를 삭제하는 경우로 나뉜다.

root 노드를 삭제하는 경우: root 노드를 삭제하는 경우에도 노드가 하나가 남기 때문에 그 유일한 자식을 root로 지정해준다. root = child 부분.
root 노드가 아닌 노드를 삭제하는 경우: parent->left 값에 삭제된 노드의 값(p == 12)이 있었다면, 혹은 parent->right 값에 삭제된 노드의 값(p == 12)가 있었다면 child의 값을 그 위치에 담아준다.

    ...
    
// 차수가 1인 경우
    // 조건문을 이렇게 쓰더라도 차수가 0인 경우가 안걸리는 이유는 if문으로 위에서 차수가 0인 경우를 걸렀기 때문에 걸리지 않게 된다.
    else if (p->left == NULL || p->right == NULL) {
        // 차수가 1인 즉, 부모가 유일한 자식을 직접 가리킬 수 있게끔 해야함. 즉, child 주소값을 저장해야함
        // 자신의 유일한 자식이 왼쪽일 수도 있고, 오른쪽일 수도 있으니까 child에 담아주자.
        // left가 NULL이 아니라면 현재 노드 p->left에 값이 있다는 뜻이니까 left 값 대입, 아니라면 p->right 값 대입
        NODE* child = (p->left != NULL) ? p->left : p->right;
        // root 노드가 삭제되는 경우
        if (parent == NULL)
            // 루트 노드가 삭제되지만 이번에는 그 루트 노드가 자식 하나를 가지고 있기 떄문에 그 자식이 새로운 루트가 된다.
            root = child;
        // root 노드가 삭제되는 경우가 아니라면 
        else {
            
            if (parent->left == p)
                parent->left = child;
            else
                parent->right = child;
        }
    }

	...
    
    
    free(p); // 차수가 0, 1, 2 어떤 경우이든 간에 노드를 삭제하니까 해당 노드를 삭제한다.

차수가 2인 삭제 구현 코드

차수가 2인 노드의 삭제는 왼쪽 서브트리 혹은 오른쪽 서브트리 중 하나의 후계자를 골라서 삭제 노드 자리에 삽입(복사)해준다.(삭제 대상인 노드의 자리에는 후계자 값으로 대체되게 된다.) 이때 어느쪽 트리를 고르냐에 따라 후계자를 고르는 방식이 조금 다르게 되는데, 왼쪽 서브트리 중에서 후계자를 고르게 된다면 가장 큰 값을 고르면 되고, 오른쪽 서브트리 중에서 후계자를 고르게 된다면 가장 작은 값을 고르면 된다. 왜냐하면 그렇게해야 이진 탐색 트리의 속성을 맞출 수 있기 때문이다.

다음 이미지를 보고 이해해보자.

차수가 2인 노드를(10) 삭제하고 왼쪽 서브트리에서 가장 큰 값(8)을 골라 삭제된 노드 자리에 대입하게 된다면 이진 탐색 트리의 속성을 모두 만족하게 된다.

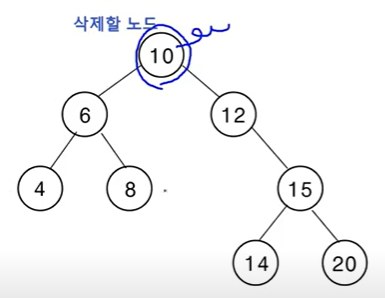
마찬가지로 오른쪽 서브트리에서 가장 작은 값(12)를 골라 삭제된 노드 자리에 대입한다. 이때 오른쪽 서브트리에서 가장 작은 값인 12를 빼게 된다면 그 자리의 노드를 삭제하고, 12번 노드는 이전에 차수가 1인 노드로 오른쪽 자식이자 서브트리인 15를 12와 다시 연결시켜주면 그제서야 이진 탐색 트리의 속성을 모두 만족하게 된다.

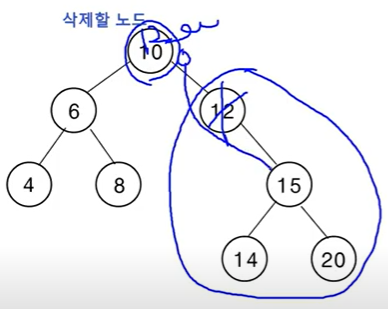
위의 예시를 보았을 때 차수가 2인 노드를 삭제하게 되고, 그 자리의 후계자를 선택한다면 차수가 0인 노드 또는 차수가 1인 노드가 선택되게 된다. 후계자로서 차수가 2인 노드는 올 수 없는 이유는 가장 작은 값, 또는 가장 큰 값을 골랐기 때문에 차수가 0 또는 1를 가질 수 밖에 없다.

위의 예시에서 삭제할 노드의 대상은 차수가 2인 '10' 노드를 제거해야 하는데 실제로 로직을 구현할 때는 후계자 노드를 삭제하고, 삭제할 노드의 대상에는 후계자 노드의 데이터 값만 복사해준다. 예를 들어 위의 예시에서 왼쪽 서브트리를 후계자로 뽑았다면 '8'이 뽑힐 것이고, 8의 노드는 지워주고, 8의 데이터 값만 삭제할 대상 노드에 데이터 값을 복사한다. 마찬가지로 오른쪽 서브트리에서 후계자로 뽑았다면 '12'가 뽑힐 것이고, 12 노드는 지워주고, 12의 데이터 값만 삭제할 대상 노드에 데이터 값을 복사한다.

...
// 차수가 2인 경우
    // 차수가 2인 경우는 별다른 조건을 걸어줄 필요 없이 else문을 걸어주면 된다.
    // 왜냐하면 앞에서 차수가 0인 경우, 1인 경우를 모두 제거했기 때문이다.
    else {
        // 후계자 노드를 골라야한다. 후계자는 왼쪽 서브트리, 오른쪽 서브트리 중 어느 것을 골라도 무방하다.
        // 참고로 후계자 노드는 차수가 0인 노드 또는 1인 노드만 골라지게 된다. 
        // 여기서는 오른쪽 서브트리에서 고르는 것을 기준으로 한다.
        NODE* succ_parent = p; // 후계자 노드의 부모
        NODE* succ = p->right; // 후계자 노드(오른쪽 서브트리에서 고르는 것을 기준으로 하기 때문에 p->right)
        
        // 오른쪽 서브트리에서 가장 작은 값을 찾아야하기 때문에, 
        // 후계자는(succ) 왼쪽 자식이 없는 노드가 나타날때까지 내려가면 된다.
        while (succ->left != NULL) {
            succ_parent = succ;
            succ = succ->left;
        }
        // 후계자 노드의 값(오른쪽 서브트리에서 가장 작은 값)을 삭제 대상의 값에 대입한다.
        p->key = succ->key;
        // 후계자인 succ는 삭제될 대상의 노드이고,
        // succ_parent->left 에는 succ가 삭제된다면 NULL 값으로 채워져야한다. 
        // 혹은 succ의 오른쪽 자식이 있다면 succ_parent 왼쪽 서브트리로 이어붙여줘야한다.
        if (succ_parent->left == succ)
            succ_parent->left = succ->right;
        
        // succ 값을 지워줘야하므로 현재 노드 p를 succ로 초기화한다.
        p = succ;
        
    }
    
    free(p); // 차수가 0, 1, 2 어떤 경우이든 간에 노드를 삭제하니까 해당 노드를 삭제한다.
    ...

이제 다 만들었으니 트리에 노드를 넣어주고, 중위순회로 데이터가 잘 뽑히는지 보자.

중위순회의 코드와 main 코드는 다음과 같다.

참고: 처음 root 노드를 넣을 땐 root 인자에 NULL를 넣어줘야 함.

처음 노드를 트리에 넣게 되면 비교 대상이 없기 때문이다.값은 정확하게 ABCDI 순으로 나오게 된다.

void inorder(NODE* root) {
    if (root == NULL)
        return;
    inorder(root->left);
    printf("%c ", root->key);
    inorder(root->right);
}

int main(void) {
    NODE* root = insertBST(NULL, 'D');
    insertBST(root, 'I');
    insertBST(root, 'A');
    insertBST(root, 'B');
    insertBST(root, 'C');
    inorder(root); printf("\n");
    return 0;
}

이진 검색 트리의 전체 코드는 아래와 같다.

전체코드

#include <stdio.h>
#include <stdlib.h>

typedef char data;
// 자기참조구조체 - 데이터부와 링크부 2개가 들어가게 된다.
typedef struct _NODE {
    char key;
    struct _NODE* left;
    struct _NODE* right;
} NODE;

// 매개변수 : NODE의 포인터, 찾을 데이터
NODE* searchBST(NODE* root, char x)
{
    NODE* p = root;
    while (p != NULL) {
        if (p->key == x)
            return p;
        else if (p->key < x)
            p = p->right;
        else
            p = p->left;
    }
    return NULL;
}

// 매개변수 : NODE의 포인터, 삽입할 노드의 key
NODE* insertBST(NODE* root, char x)
{
    NODE* p = root;
    // root가 NULL 일수도 있으므로 parent를 바로 root의 값을 참조하는 것이 아닌, NULL 값으로 초기화를 진행한다.
    NODE* parent = NULL;
    while (p != NULL) {
        parent = p; // p의 발자취를 따라가면서 parent에 p의 이전 값을 담음
        if (p->key == x)
            return p;
        else if (p->key < x)
            p = p->right;
        else
            p = p->left;
    }

    // 탐색에 실패하였을 때, 비로소 삽입할 수 있는 시점
    // 새 노드 할당
    NODE* newNODE = (NODE*)malloc(sizeof(NODE));
    newNODE->key = x;                      // 삽입할 key값
    newNODE->left = newNODE->right = NULL; // 단말 노드가 될 것이기 때문에 left, right NULL 값을 넣는다.

    // parent의 자식으로 새 노드 붙이기
    /*
    root가 NULL 일수도 있으므로 parent가 NULL이 아닐경우에만 삽입 과정을 수행한다.
    root가 NULL 이라면 위의 while문을 한번도 돌지 않을 것이고(같은 말로 탐색을 한번도 수행을 하지 않을 것이고),
    탐색을 한번도 수행하지 않았다면 parent의 값도 NULL로 되어있음
    */

    if (parent != NULL) {
        // 왼쪽, 오른쪽 삽입 위치 구분
        if (parent->key < newNODE->key)
            parent->right = newNODE;
        else
            parent->left = newNODE;
    }
    return newNODE;
}

// 매개변수 : NODE의 포인터, 삽입할 노드의 key
NODE* deleteBST(NODE* root, char x) {
    NODE* p = root;
    // root가 NULL 일수도 있으므로 parent를 바로 root의 값을 참조하는 것이 아닌, NULL 값으로 초기화를 진행한다.
    NODE* parent = NULL;
    while ((p != NULL) && (p->key != x)) { // 찾는 노드가 없다는 걸 확인한 것도 아니고, 키를 찾은 것도 아닌 동안은 계속 반복
        parent = p; // p의 발자취를 따라가면서 parent에 p의 이전 값을 담음
        if (p->key < x)
            p = p->right;
        else
            p = p->left;
    }
    // 찾는 노드가 없을 땐
    // 노드 찾는데 실패했기 때문에 받은 그대로를 반환해준다.
    if (p == NULL) {
        printf("찾는 노드가 없습니다.\n");
        return root;
    }

    // 차수가 0인 경우(2가지 대분류 필요)
    // 1. root 를 삭제하는 경우
    // 2. root 가 아닌 노드를 삭제하는 경우
    if (p->left == NULL && p->right == NULL) {
        // 현재 노드가 root 인 경우
        // 91번째 라인 'p->key != x' 의 찾는 값이 일치하여서 while문을 돌지 않게된다면, parent의 값은 NULL로 유지하게 된다.
        // 즉, 간단하게 말하면 root노드의 차수가 0이라면 parent의 값은 NULL임
        if (parent == NULL)
            root = NULL;
        // 루트가 아닌데 차수가 0인 경우
        // 그 이외의 경우에는 즉, root가 아닌 노드가 삭제될 경우에는 parent의 포인터를 고쳐주어야 한다.
        // parent가 삭제될 노드의 left 또는 right로 현재 삭제될 노드(p)를 가리키고 있다.
        else {
            if (parent->left == p)
                parent->left = NULL;
            else
                parent->right = NULL;
        }

    }
    // 차수가 1인 경우
    // 조건문을 이렇게 쓰더라도 차수가 0인 경우가 안걸리는 이유는 if문으로 위에서 차수가 0인 경우를 걸렀기 때문에 걸리지 않게 된다.
    else if (p->left == NULL || p->right == NULL) {
        // 차수가 1인 즉, 부모가 유일한 자식을 직접 가리킬 수 있게끔 해야함. 즉, child 주소값을 저장해야함
        // 자신의 유일한 자식이 왼쪽일 수도 있고, 오른쪽일 수도 있으니까 child에 담아주자.
        // left가 NULL이 아니라면 현재 노드 p->left에 값이 있다는 뜻이니까 left 값 대입, 아니라면 p->right 값 대입
        NODE* child = (p->left != NULL) ? p->left : p->right;
        // root 노드가 삭제되는 경우
        if (parent == NULL)
            // 루트 노드가 삭제되지만 이번에는 그 루트 노드가 자식 하나를 가지고 있기 떄문에 그 자식이 새로운 루트가 된다.
            root = child;
        // root 노드가 삭제되는 경우가 아니라면 
        else {

            if (parent->left == p)
                parent->left = child;
            else
                parent->right = child;
        }
    }
    // 차수가 2인 경우
    // 차수가 2인 경우는 별다른 조건을 걸어줄 필요 없이 else문을 걸어주면 된다.
    // 왜냐하면 앞에서 차수가 0인 경우, 1인 경우를 모두 제거했기 때문이다.
    else {
        // 후계자 노드를 골라야한다. 후계자는 왼쪽 서브트리, 오른쪽 서브트리 중 어느 것을 골라도 무방하다.
        // 참고로 후계자 노드는 차수가 0인 노드 또는 1인 노드만 골라지게 된다. 
        // 여기서는 오른쪽 서브트리에서 고르는 것을 기준으로 한다.
        NODE* succ_parent = p; // 후계자 노드의 부모
        NODE* succ = p->right; // 후계자 노드(오른쪽 서브트리에서 고르는 것을 기준으로 하기 때문에 p->right)

        // 오른쪽 서브트리에서 가장 작은 값을 찾아야하기 때문에, 
        // 후계자는(succ) 왼쪽 자식이 없는 노드가 나타날때까지 내려가면 된다.
        while (succ->left != NULL) {
            succ_parent = succ;
            succ = succ->left;
        }
        // 후계자 노드의 값(오른쪽 서브트리에서 가장 작은 값)을 삭제 대상의 값에 대입한다.
        p->key = succ->key;
        // 후계자인 succ는 삭제될 대상의 노드이고,
        // succ_parent->left 에는 succ가 삭제된다면 NULL 값으로 채워져야한다. 
        // 혹은 succ의 오른쪽 자식이 있다면 succ_parent 왼쪽 서브트리로 이어붙여줘야한다.
        if (succ_parent->left == succ)
            succ_parent->left = succ->right;

        // succ 값을 지워줘야하므로 현재 노드 p를 succ로 초기화한다.
        p = succ;

    }

    free(p); // 차수가 0, 1, 2 어떤 경우이든 간에 노드를 삭제하니까 해당 노드를 삭제한다.
}

void inorder(NODE* root) {
    if (root == NULL)
        return;
    inorder(root->left);
    printf("%c ", root->key);
    inorder(root->right);
}

int main(void) {
    NODE* root = insertBST(NULL, 'D');
    insertBST(root, 'I');
    insertBST(root, 'A');
    insertBST(root, 'B');
    insertBST(root, 'C');
    inorder(root); printf("\n");
    return 0;
}

Ref

[자료구조] 이진 탐색 트리 : 개념과 구현(C언어)

다음글이 없습니다.

이전글이 없습니다.